中2 平行と合同 「平行と合同」の単元では、平行線や角の性質、図形の合同について学習します。 特につまずきやすいのは合同の証明です。 正確な証明が書けるようになるには練習が必要で、時間がかかります。 苦手意識があるうちは、「はじめに証明 中2数学 練習プリントが無料でダウンロード・印刷できます。 正三角形、正方形を 利用した合同の証明 直角三角形の 合同の証明 等積変形 四角形 平行四辺形の性質 平行四辺形に なるための条件 特別な平行四辺形 確率 確率の基礎 2個のさいころ カード コイ 中2数学:証明問題(平行な2直線→三角形の合同を用いた証明) 中2数学:逆(仮定と結論の入れ替え、反例の示し方) 中2数学:二等辺三角形の基礎(角の大きさ、二等分線、合同を用いた証明) 中2数学:直角三角形の合同条件と証明問題 コメントを残す コメントをキャンセル メール

不可思议的托勒密定理 证明
垂直二等分線 証明 中2
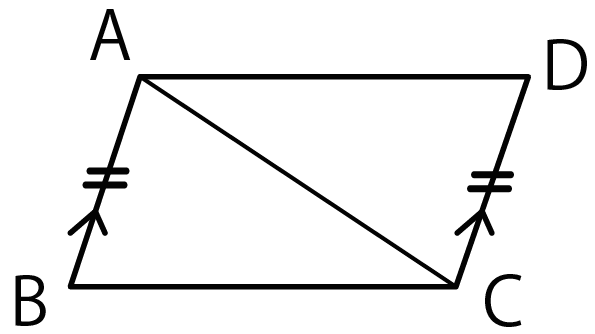
垂直二等分線 証明 中2-「育成中」左腕が力証明 高橋、奥川に続き好投―プロ野球cs・ヤクルト 11/11(木) 2333 配信 59 力投するヤクルト先発の高橋=11日、神宮 中2数学図形の証明問題を攻略できる6つのコツ っていう記事をかいてみたよ。 証明問題のせいで数学が嫌いになりそう、 ってときに参考にしてみてね笑 数学の証明問題を攻略するための6つのコツ つぎの例題をときながら解説するよ。 ab = dc、ab // dcの abcと cdaがあったとし




初中几何证明辅助线有哪些 楠木轩
数学 証明 中2 635K views Discover short videos related to 数学 証明 中2 on TikTok Watch popular content from the following creators 淳せんせい ️📖数学理科(@jun_sensei), 淳せんせい ️📖数学理科(@jun_sensei), 学習塾We'lll(@jukuwelll), けいたくチャンネル(@keitaku_channel), いっし🤗🙈=男14中学校数学 三角形の内角の和が180°になることの証明 管理人 2月 18, 19 中学2年では三角形の内角や外角の性質を利用して、図形の角度中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード・印刷 教材の新学習指導要領への対応について ただいま、ちびむすドリル中学生では、公開中の中学生用教材の新学習指導要
中2数学:証明問題(平行な2直線→三角形の合同を用いた証明) 中2数学:二等辺三角形の証明問題 3 COMMENTS ナオドット先生 年12月16日 質問があればお気軽にどうぞ。100%返答します。 返信する rei 21年2月22日 x+1=3ならばx=2であるの逆は成り立ちますか? 返信する ナオドット先生 21年2年生 5 図形の性質と証明 この証明のあと,図1と形の違う図2のような平行四辺形ABCDについても,同じようにAF=C Eとなるかどうかを考えてみたところ,下のアからエのような意見が出ました。正しいものを1つ 選びなさい。プリントは追加、変更していきます。また、問題の解説も今後増やしていきます。式の計算 単項式と多項式 式の加法・減法 単項式の乗法・除法 いろいろな計算 等式の変形 式の値式の計算の利用 式による証明 図形への利用連立方程式 2元1次方程式 連立方程式(加減法) 連立方程式(代入法
今回は中2で学習する 『合同な図形』の基本性質について解説していくよ! 図形と証明 229 二等辺三角形の定義と性質をサクッと確認しておこう! 図形と証明 平行四辺形の角度、辺の長さ求め方を問題解説! 図形と証明 3分なるほど!三角形の内角、外角の性質 中2数学の最難関!図形の証明が登場! 保護者 連立方程式は反復練習で何とかなりそうだけれど、やっぱり証明は難しい気がします。 教室長 図形の証明は好ききらいが分かれますね。数学がニガテなお子さんの中にも証明は得意なお子さんがいたり、逆に比較的数学が得意なのに証明はHello School 数学 問題集(ハロ数) 中2 合同と証明 インターネット上で中学校の数学を勉強できるよ。 自分のノートに問題を解いて、生徒のイラストをクリックすれば解答のページが出てくるから、 丸付けをして、間違えた問題はもう一度やり直したり、解説を理解していこうね。 1. 次の各



Studydoctor作図の証明 中2数学 Studydoctor




Leetcode 链表中是否存在环的证明问题 Segmentfault 思否
合同の証明1 1 右の図でAC=BD、AD=BCのとき ABC≡ BADとなることを証明せよ。 2 右の図で、AB//DC, AB=DCならば、 ABO≡ DCOとなることを証明せよ。 3 AB=AC, AD=AEのとき 中2数学 中2数学「証明のしくみと進め方」の問題 どこよりも簡単な解き方・求め方 kazunokazu 21年8月25日 今日の数学の授業 むずかしかったな 宿題かんたんに できるかな? かずのかず 数学で何か、 こまってますか? 「安心してください!」 宿題なら この記事を読んだら中学2年では三角形の内角や外角の性質を利用して、図形の角度を求める問題がよく出題されます。 そこで重要になるのが「どんな ホーム;



九章算术 中立体图形 羨除 体积公式的证明 尚书坊




初中几何证明辅助线有哪些 楠木轩
・\(2\) つの正三角形が重なっている(例題1) ・\(2\) つの正三角形が重なっていない(例題2) このときの「\(2\) つの三角形の合同の証明」は、ほぼ同じ流れになりますが、 \(2\) つの辺の間の角が等しいことを示す箇所だけ微妙に異なります。数学 証明 中2 587K 回視聴 TikTokで数学 証明 中2関連のショートムービーを探索しよう このクリエイターの人気コンテンツを見てみよう:淳せんせい ️📖数学理科(@jun_sensei), 淳せんせい ️📖数学理科(@jun_sensei), 学習塾We'lll(@jukuwelll), 勉強のおとも(@0tomowith), 学習塾We'lll(@jukuwelll) NYマラソン2年ぶり開催 参加条件に接種証明など 0804 新型コロナの影響で昨年は中止されたニューヨークマラソンが2年ぶりに開催され



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく




初识 零知识 与 证明 Secbit Blog
これをどのように証明すればいいのでしょうか。 0 回答 QT 1年以上前 (2n1)(2m1) =2n2m2 =2(nm1) nm1は整数なので2(nm1)は偶数である。 よって奇数と奇数の和は偶数である。 この問題の場合は,必ず文字は2種類使うこと。 文字が1つでいいのは,連続する奇数や連続する偶数,連続する整数証明を書き始める前に、どんなふうに証明ができるのか、頭の中で解いておこう。 問題文の中にあるヒントは図に書き込む 。そして、よく図を見て、 ほかに手がかりがないか探す んだよね。 例題の場合、問題文から、 AECと BEDについて AE=BE、CE=DE が分かっているね。 でも、2ルート2が無理数であることの4通りの証明 レベル ★ 入試対策 式の計算 更新日時 2 \sqrt {2} 2 は無理数である。 より一般に,平方数でない正の整数




中2数学 証明とは 例題編 映像授業のtry It トライイット




数学 相似三角形 Hl判定 的证明 哔哩哔哩
正三角形の利用と合同の証明中2数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・証明の手順に慣れよう ・三角形の性質を理解しよう 完璧じゃなかったら授業動画を見よう やる気先生の授業動画 単元 証明, 「図形の合同証明でかなり出てくる、メジャーな合同条件や定理、定義をまとめました。」, 学年 中学2年生, キーワード 図形,合同条件,定理,定義,合同証明,中2,数学,math<前:L33 合同条件と証明の進め方(3)の問題 『 第4章 図形の調べ方 』 の復習テスト の解答:次> 中1数学・練習問題一覧 中2数学・練習問題一覧 中3数学・練習問題一覧




Je Voulais Le Plus 自学中2 国語自学中2 ネタ




中2 数学 中2 証明 中学生 数学のノート Clearnote
範囲:中2証明,中3相似 難易度:★★★★★ <問題> <PDF,解答例はこちら↓↓> » more > Tweet comment () @ 平面(証明メイン) » 高校入試 数学 良問・難問 高校受験の良問(難問)無料数学プリント(PDF)を配布 最新記事 TOPページ (21年都立西)大学入試みたいな整数問題 数学、中2数学、四角形の性質と証明 タグ 数学 証明 中2 2年生数学 平行四辺形 性質 平行四辺形証明 図形証明 証明問題 平行四辺形の性質 中1数学 前の記事 一次方程式の文章題ー割合に関する問題 16年8月7日 中2数学 次の記事 三角形の角度 16年8月82年生 5 図形の性質と証明 次の(1),(2)の各問いに答えなさい。 (1) 前の証明のまちがいは,下に示した の中にあります。まちがっている部分を, 解答用紙 の中に下線( )をひいて示しなさい。 (2) 上の証明の の中を正しく書き直しなさい。



角平分线 三角形的证明ppt 第2课时 第一ppt




数学 中2 60 証明のしくみ Youtube
今回は、中2で学習する 証明問題の書き方 について解説していきます。 証明問題って苦手な人が多いよね(^^;問題集 3年間のまとめ(メビリス) 3年間のまとめ2(メビリス2) 一次方程式uox問題集 連立方程式uxy問題集 一次関数と図形 放物線パラボリック問題集 規則性ルール問題集 速さ系の苦手な人へ 動画シリーズ 差がつく問題・超快速思考・気になる入試問題を動画でご案内し動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




全等三角形輔助線之角平分線的四大模型 雪花新闻




世界一わかりやすい数学問題集中2 5章 図形の性質と証明
相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、 「2組の辺の比とその間の角が等しい」 という条件です



1




新课标 初中数学全等三角形证明题50道 考试必考 务必打印收藏



2 2直接证明与间接证明 人教版高中选修2 2数学电子课本 数九网
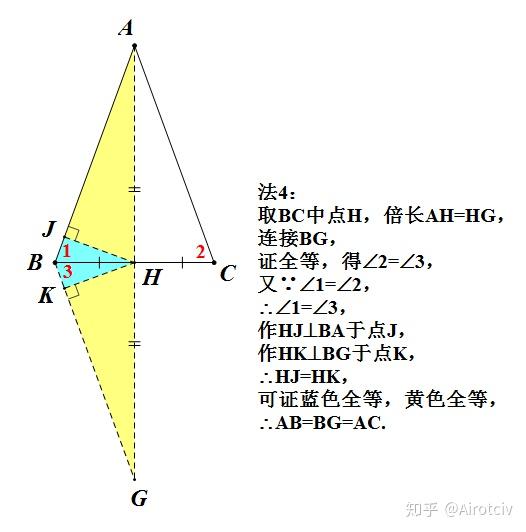



源于课堂的等腰三角形判定证明多种解法 证明等腰三角形的方法 名欧网




09垂直平分线的性质与判定三角形的证明初中数学初二 Youtube
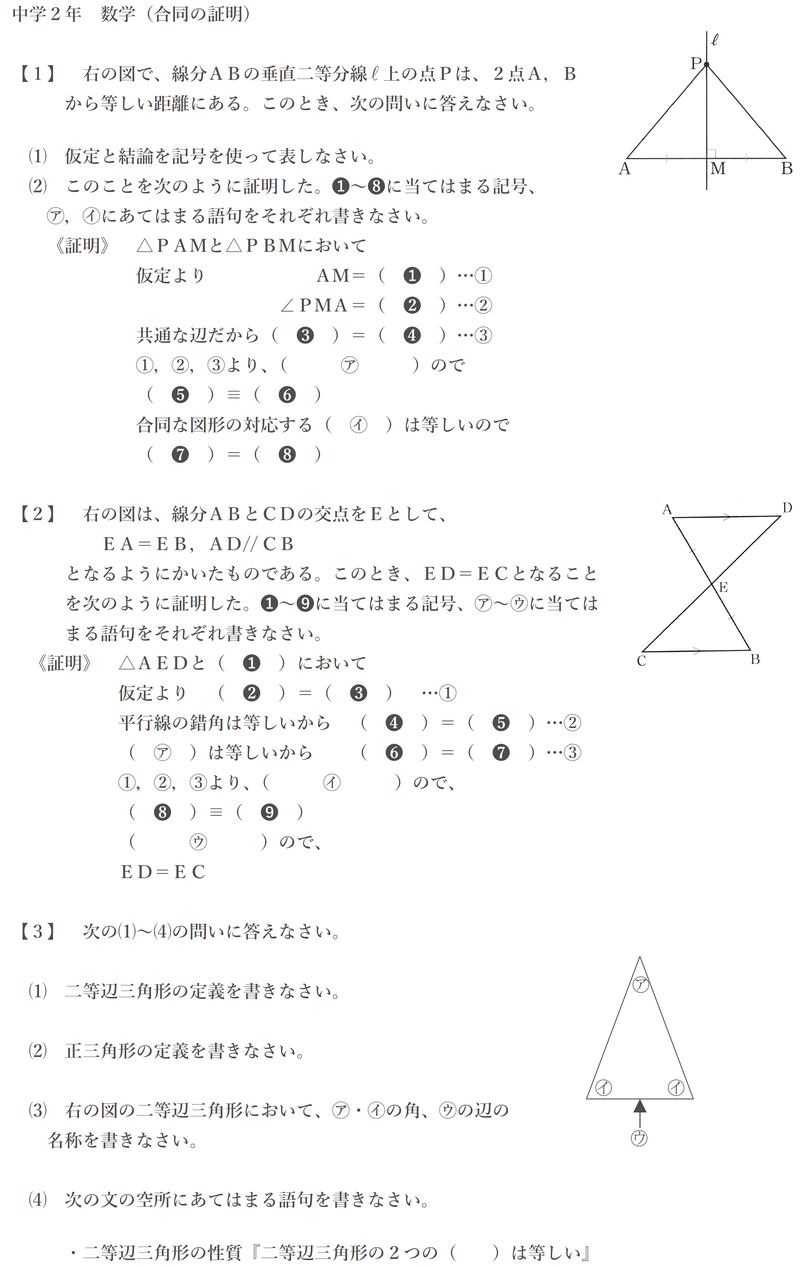



中2数学 三角形の合同の証明の流れ 3学期期末テスト用 赤城 ᐡᐤᐡ
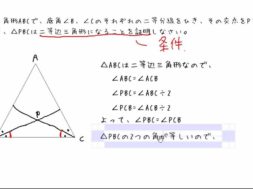



中2数学 08 6 二等辺三角形になることの証明 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



北京初二数学 初二几何中的证明 你真的懂吗 家长论坛 家长交流社区 北京小升初 北京学区房 北京幼升小幼儿入园门户网站



北京初二数学 初二几何中的证明 你真的懂吗 家长论坛 家长交流社区 北京小升初 北京学区房 北京幼升小幼儿入园门户网站




中2 中2数学 三角形の証明 中学生 数学のノート Clearnote




不可思议的托勒密定理 证明



八年级三角形全等证明 西瓜视频搜索



初中三角形中线定理证明三角形中线定理的定理证明 朵拉利品网



中2数学 通年用問題集 8章 合同の証明演習




积分第二中值定理用罗尔定理证明 高数 怎么用罗尔定理证明拉格朗日中值定理 三人行教育网 Www 3rxing Org



1



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor




中学数学 証明問題 直角三角形 Youtube



北京初二数学 初二几何中的证明 你真的懂吗 家长论坛 家长交流社区 北京小升初 北京学区房 北京幼升小幼儿入园门户网站




高二数学寒假预习 数学归纳法在证明数学命题中的应用 三好网



北京初二数学 初二几何中的证明 你真的懂吗 家长论坛 家长交流社区 北京小升初 北京学区房 北京幼升小幼儿入园门户网站
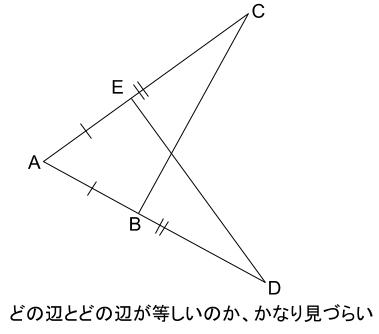



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su




世界一わかりやすい数学問題集中2 4章 平行と合同と証明
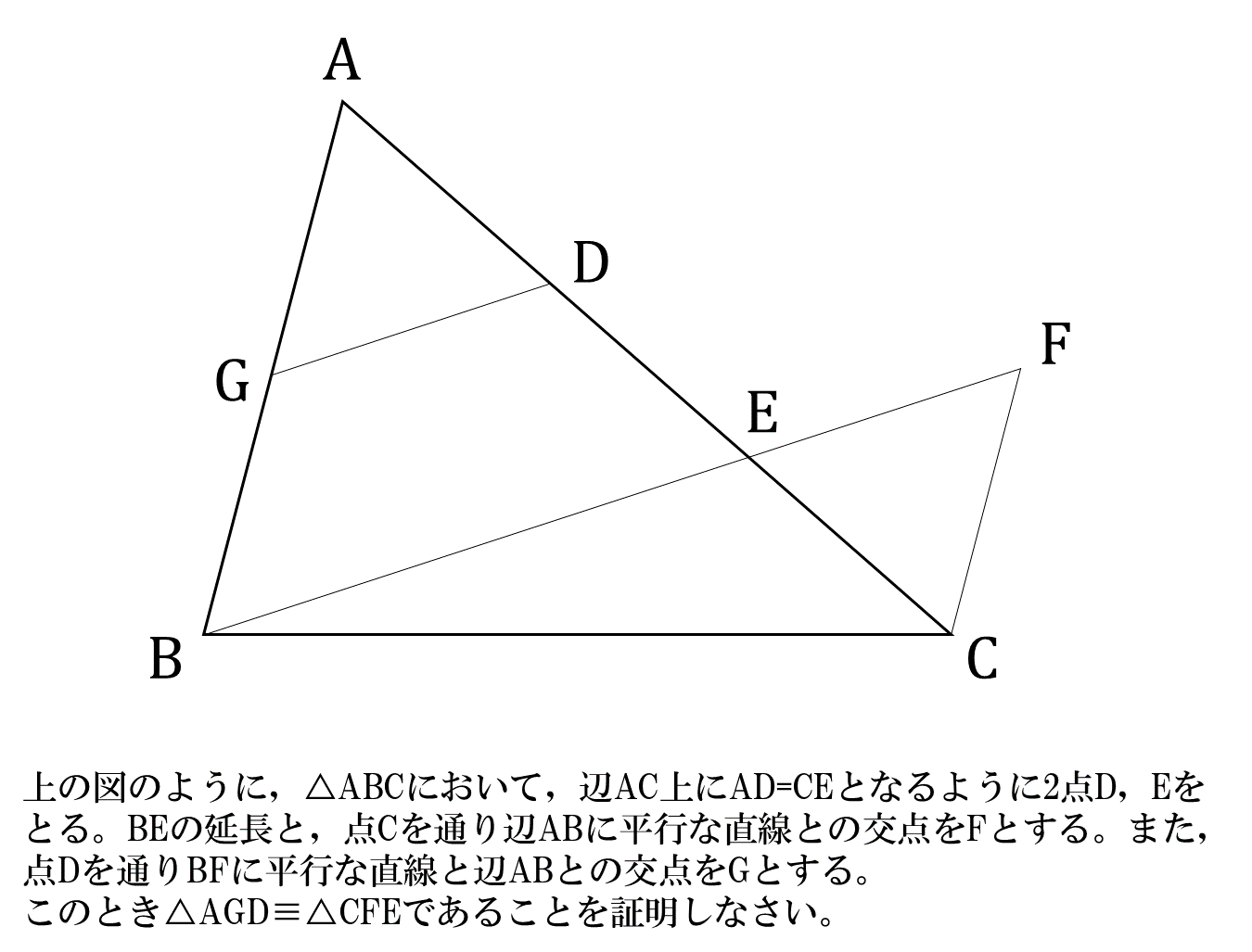



数学 中学証明問題を解く4つのポイント
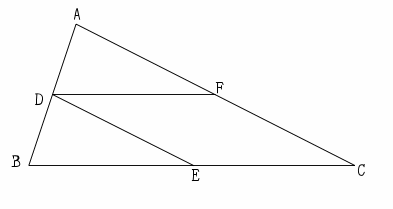



合同の証明2



七年级数学几何难题练习题 含答案 小初高题库试卷课件教案网



立派な 中学生2 年数学 ぬりえ壁紙hd




几何中证明四点共圆的常用方法有哪些 数学




中2 証明 中二 中学生 数学のノート Clearnote
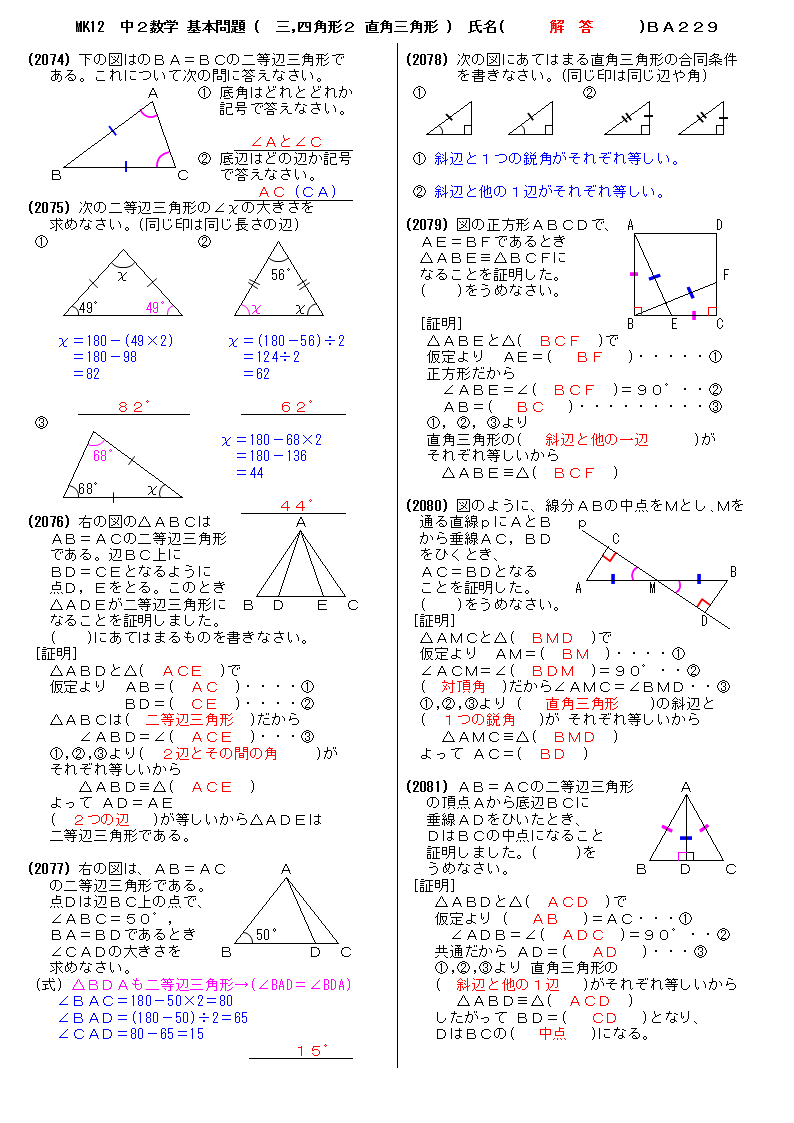



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形



初中数学48个解题模型 Csdn




教学思考 几何证明分析方法 2 简书




高考数学中 数列不等式的证明 一定要掌握的6个答题模板 哔哩哔哩




三角形triangle




中2数学 証明とは 練習編 映像授業のtry It トライイット



三角形中位线定理的证明方法 初三网




21年初中数学圆专题09 圆中的切线证明问题 网易订阅




初中几何 三角形中常用辅助线总结及例题解析 楠木轩




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step



数学证明 快懂百科
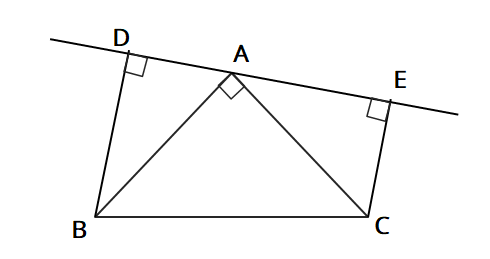



中2数学 直角三角形の合同の証明 応用問題 デルココ



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ



线线垂直的证明方法 万图壁纸网




二维柯西不等式的几种证明方法 参考网



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor
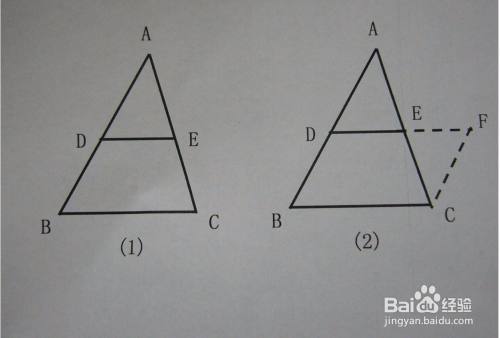



三角形中位线的三种证明方法 百度经验



全等三角形证明方法归纳 典例详解几种辅助线做法 含思路分析 电竞主播网




Leetcode 链表中是否存在环的证明问题 Segmentfault 思否



初一数学几何难题练习题 含答案 提高能力专用 线段




如何证明 直线与平面垂直的判定定理 知乎



Studydoctor正三角形の利用と合同の証明 中2数学 Studydoctor




中2証明問題について Clearnote
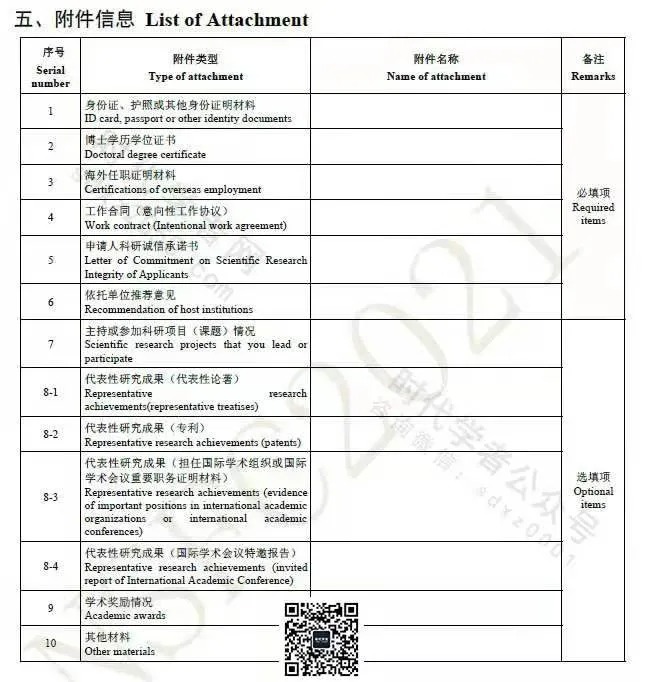



形式审查与评审中 海外优青申请人系统状态更新了 时代学者




これで点が取れる 単元末テスト中2数学 5章 図形の性質と証明




19年全国统一高考数学试卷理科新课标 静雅斋数学 博客园




初中几何辅助线的做法原来还有技巧的 2 网易订阅




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形




平行线的证明测试题下载 Word模板 爱问共享资料



中2の数学の証明問題なんですが 英語の順番って違くてもいいん Yahoo 知恵袋
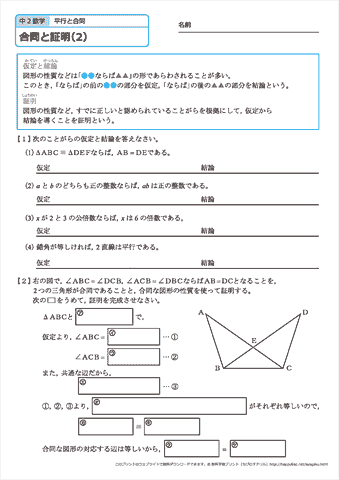



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




掌握這些初中幾何證明題知識點 再也不怕中考數學證明題丟分了 每日頭條



Studydoctor平行線の性質と証明 中2数学 Studydoctor




在穆罕默德 凯斯一案中 2名刑事调查局拘留中心官员被




数学中2 中学生 数学のノート Clearnote




初中数学几何证明题的解题技巧研究 参考网



三角形的中位线教案 三角形的中位线教案资料 新学语文网
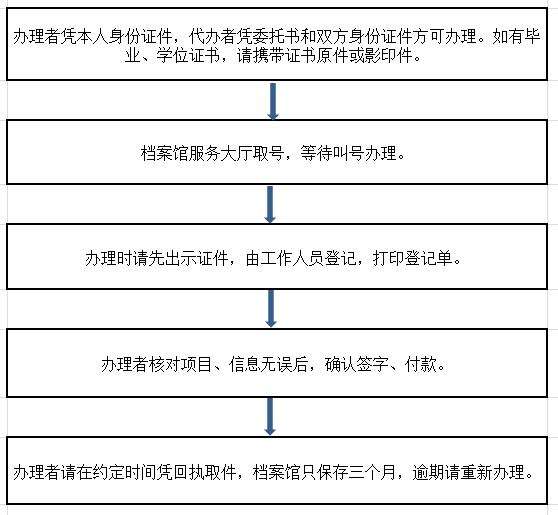



上海大学档案馆办理中英文各类证明流程 上海成绩单打印 日月兼程办事



三角形的证明题 万图壁纸网



三角形内角和定理 平行线的证明ppt课件 第2课时 第一ppt




中学2年 数学 証明まとめ 中学生 数学のノート Clearnote
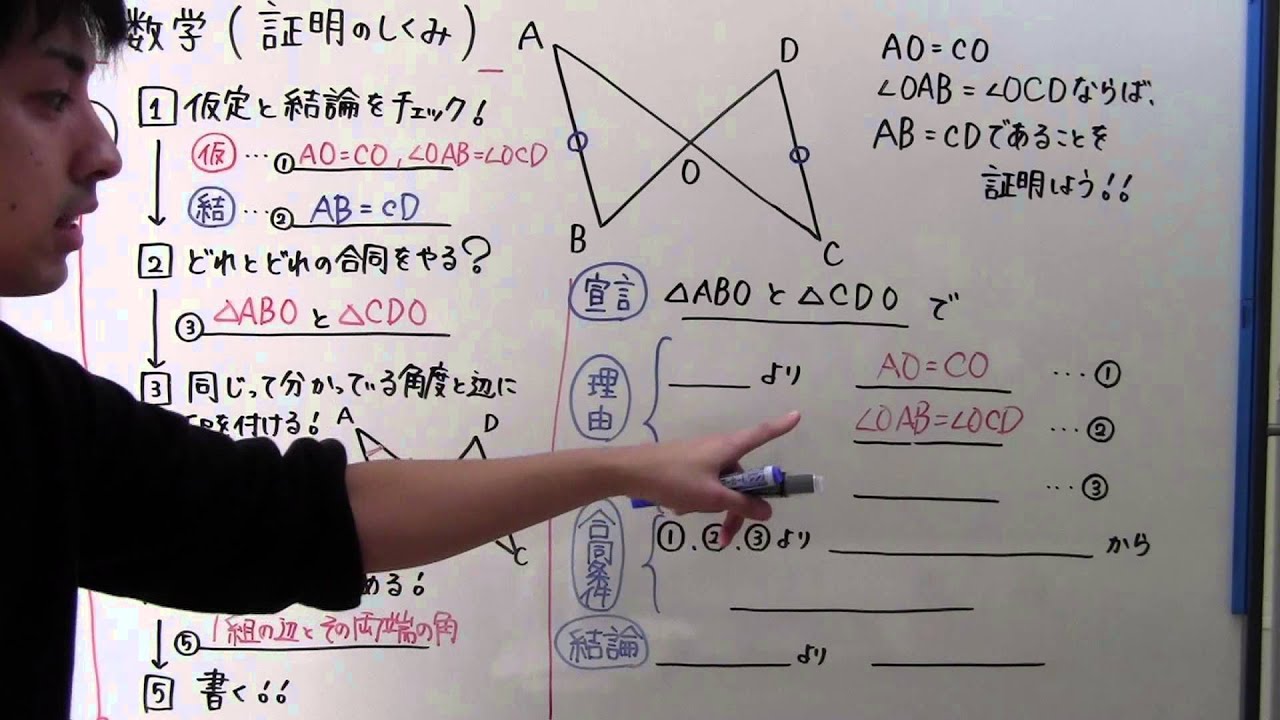



中2 数学 中2 60 証明のしくみ Youtube




数学 中2 61 証明チャレンジ Lv 1 Youtube




数理逻辑 证明及其限度 第2版 逻辑与形而上学教科书系列




中2 中2 数学 5章 図形の性質と証明 プレイカラー 中学生 Clearnote
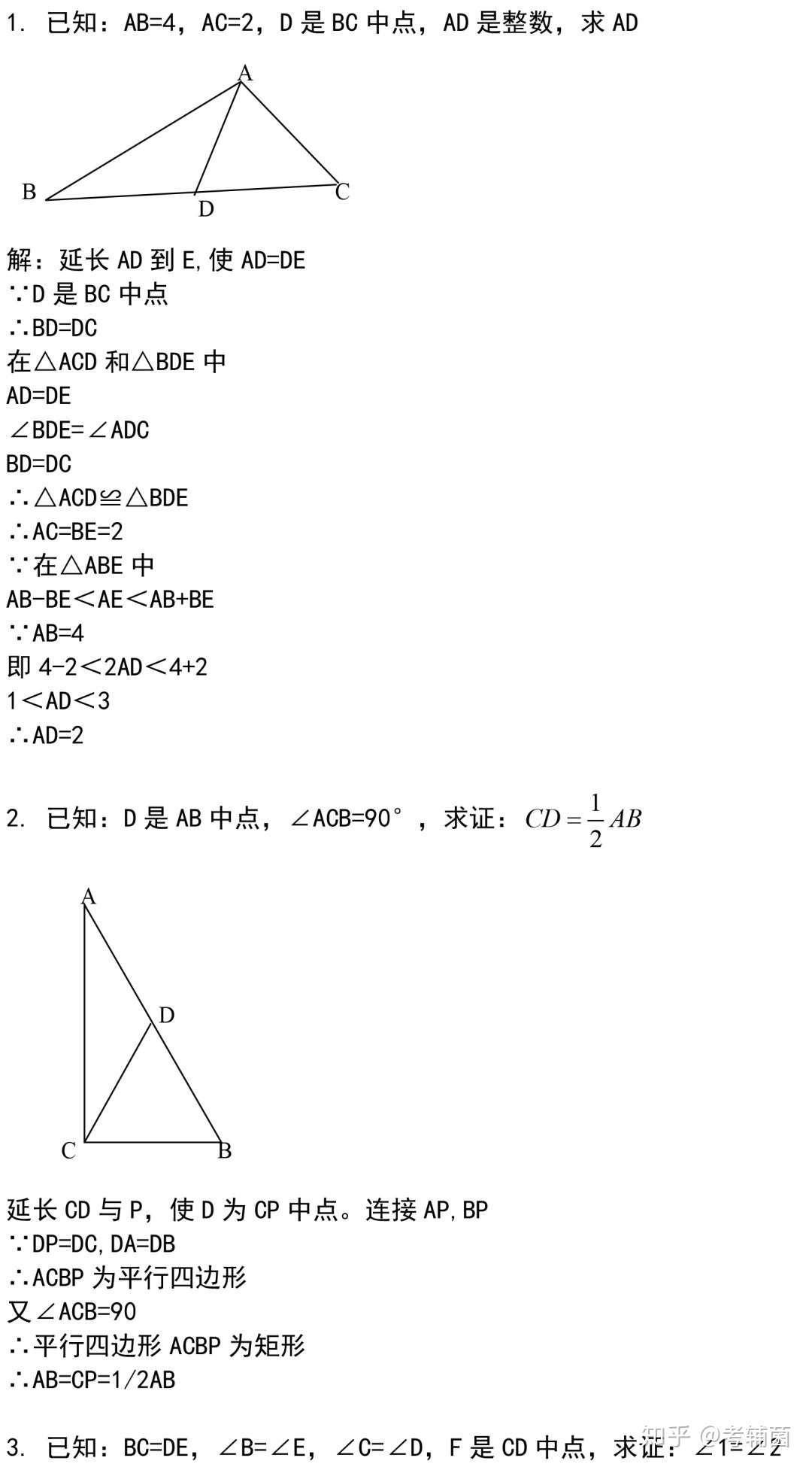



44道经典的三角形证明题 全部做完期末证明题满分 还不来看 知乎




上数学合同条件 ニスヌーピー壁紙
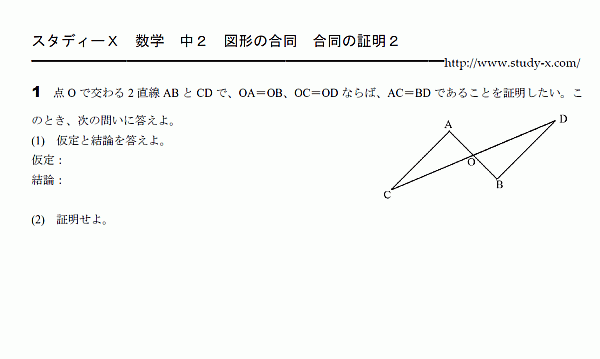



最も人気のある 三角形合同証明 ニスヌーピー壁紙




上中2 数学証明三角形4608 中2 数学証明三角形問題




21年初中数学圆专题09 圆中的切线证明问题 网易订阅
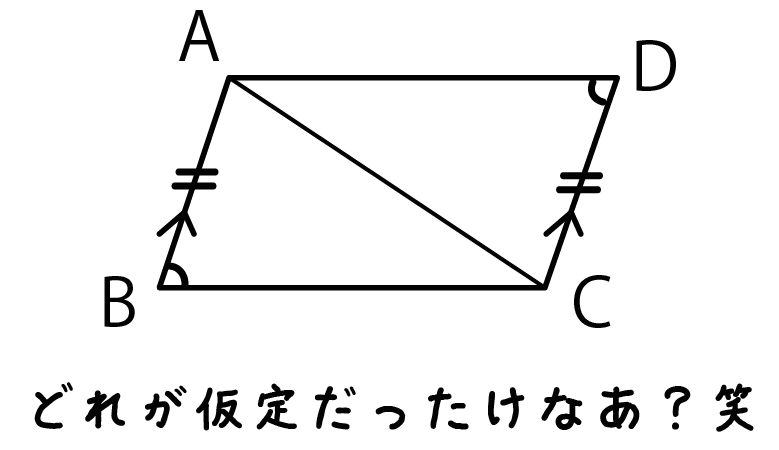



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく
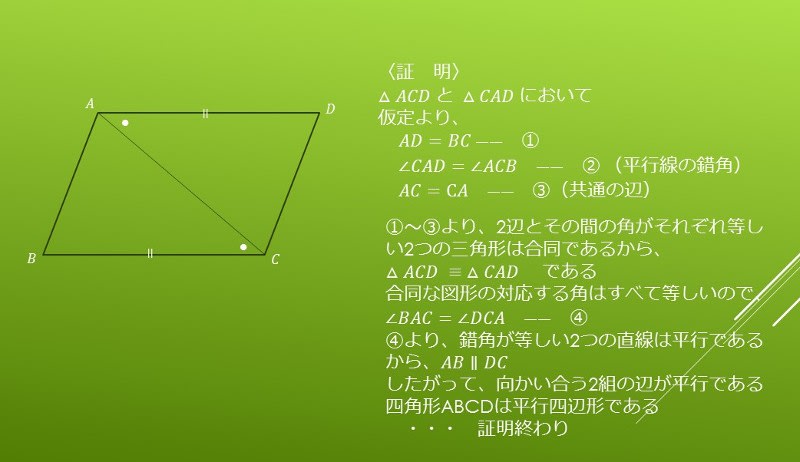



中2数学 図形の証明問題では様々な図形の性質を理解することが大切 中学生 受験対応 英語 数学 学習講座




無料 中2数学 基本解説 問題プリント 226 図形6 証明のしくみと根拠



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく



初中数学几何证明题的答题技巧和解题思路 条件



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ



初一数学几何难题练习题 含答案 提高能力专用 线段




译 哥德尔的发现 What Godel Discovered Brethland S Blog




正弦定理证明 静雅斋数学 博客园



0 件のコメント:
コメントを投稿